Probability distribution of statistics of a large number of samples selected from the population is called sampling distribution. When we increase the size of sample, sample mean becomes more normally distributed around population mean. The variability of the sample decreases as we increase sample size.
- A sampling distribution is a statistic that is arrived out through repeated sampling from a larger population.
- It describes a range of possible outcomes that of a statistic, such as the mean or mode of some variable, as it truly exists a population.
- The majority of data analyzed by researchers are actually drawn from samples, and not populations.
Statistical sampling is used quite often in statistics. In this process, we aim to determine something about a population. Since populations are typically large in size, we form a statistical sample by selecting a subset of the population that is of a predetermined size. By studying the sample we can use inferential statistics to determine something about the population.
A statistical sample of size n involves a single group of n individuals or subjects that have been randomly chosen from the population. Closely related to the concept of a statistical sample is a sampling distribution.
Origin of Sampling Distributions
A sampling distribution occurs when we form more than one simple random sample of the same size from a given population. These samples are considered to be independent of one another. So if an individual is in one sample, then it has the same likelihood of being in the next sample that is taken.
We calculate a particular statistic for each sample. This could be a sample mean, a sample variance or a sample proportion. Since a statistic depends upon the sample that we have, each sample will typically produce a different value for the statistic of interest. The range of the values that have been produced is what gives us our sampling distribution.
Sampling Distribution for Means
For an example, we will consider the sampling distribution for the mean. The mean of a population is a parameter that is typically unknown. If we select a sample of size 100, then the mean of this sample is easily computed by adding all values together and then dividing by the total number of data points, in this case, 100. One sample of size 100 may give us a mean of 50. Another such sample may have a mean of 49. Another 51 and another sample could have mean of 50.5.
The distribution of these sample means gives us a sampling distribution. We would want to consider more than just four sample means as we have done above. With several more sample means we would have a good idea of the shape of the sampling distribution.
Understanding Sampling Distribution
A lot of data drawn and used by academicians, statisticians, researchers, marketers, analysts, etc. are actually samples, not populations. A sample is a subset of a population. For example, a medical researcher that wanted to compare the average weight of all babies born in North America from 1995 to 2005 to those born in South America within the same time period cannot within a reasonable amount of time draw the data for the entire population of over a million childbirths that occurred over the ten-year time frame. He will instead only use the weight of, say, 100 babies, in each continent to make a conclusion. The weight of 200 babies used is the sample and the average weight calculated is the sample mean.
Now suppose that instead of taking just one sample of 100 newborn weights from each continent, the medical researcher takes repeated random samples from the general population, and computes the sample mean for each sample group. So, for North America, he pulls up data for 100 newborn weights recorded in the US, Canada and Mexico as follows: four 100 samples from select hospitals in the US, five 70 samples from Canada and three 150 records from Mexico, for a total of 1200 weights of newborn babies grouped in 12 sets. He also collects a sample data of 100 birth weights from each of the 12 countries in South America.
Each sample has its own sample mean and the distribution of the sample means is known as the sample distribution.
The average weight computed for each sample set is the sampling distribution of the mean. Not just the mean can be calculated from a sample. Other statistics, such as the standard deviation, variance, proportion, and range can be calculated from sample data. The standard deviation and variance measure the variability of the sampling distribution.
The number of observations in a population, the number of observations in a sample and the procedure used to draw the sample sets determine the variability of a sampling distribution. The standard deviation of a sampling distribution is called the standard error. While the mean of a sampling distribution is equal to the mean of the population, the standard error depends on the standard deviation of the population, the size of the population and the size of the sample.
Knowing how spread apart the mean of each of the sample sets are from each other and from the population mean will give an indication of how close the sample mean is to the population mean. The standard error of the sampling distribution decreases as the sample size increases.
Why Do We Care?
Sampling Distributions may seem fairly abstract and theoretical. However, there are some very important consequences from using these. One of the main advantages is that we eliminate the variability that is present in statistics.
For instance, suppose we start with a population with a mean of μ and standard deviation of σ. The standard deviation gives us a measurement of how spread out the distribution is. We will compare this to a sampling distribution obtained by forming simple random samples of size n. The sampling distribution of the mean will still have a mean of μ, but the standard deviation is different. The standard deviation for a sampling distribution becomes σ/√ n.
Thus we have the following
- A sample size of 4 allows us to have a sampling distribution with a standard deviation of σ/2.
- A sample size of 9 allows us to have a sampling distribution with a standard deviation of σ/3.
- A sample size of 25 allows us to have a sampling distribution with a standard deviation of σ/5.
- A sample size of 100 allows us to have a sampling distribution with a standard deviation of σ/10.
So How Does It Work?
Let me try and explain the basic line of thinking with a simple example. The Hague has roughly 500,000 inhabitants. I’d like to know what percentage of this population is single. Since I can’t ask 500,000 people, I approached 20 of them and asked if they consider themselves single. Like so, I found 6 singles and 14 non singles in my sample of 20. I visualized it below.
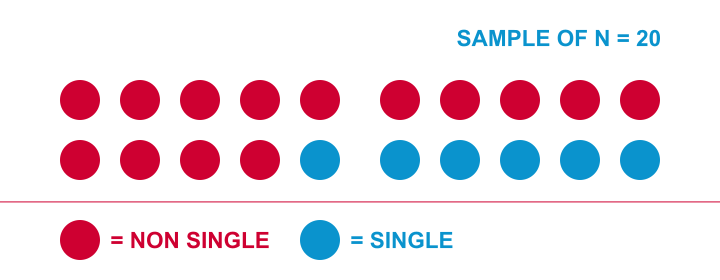
A more common way to visualize this result is the frequency distribution shown below. Note that it holds the exact same information as the previous figure.
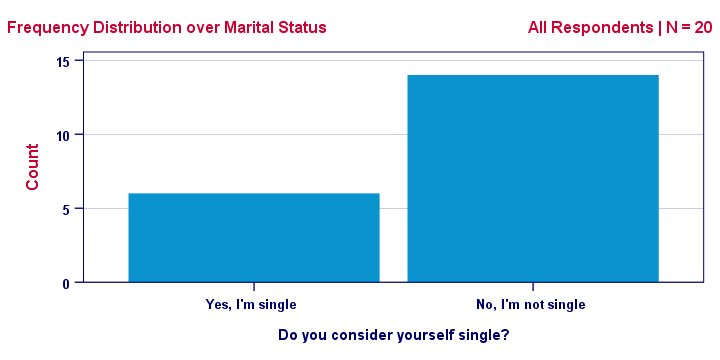
This chart shows how our sample frequencies are distributed (hence “frequency distribution”) over our values: value blue has a frequency of 6, red 14. We could even summarize our outcome as a single number: 30% of our 20 respondents are single.
Are Samples Worthless?
Right, so given my sample of N = 20 and the outcome of 30% singles, what can I conclude -if anything- about my target population, the 500,000 inhabitants of the Hague?
Can I conclude that 30% of the 500,000 inhabitants are single? Or could it be 40% as well? Or 10%? Or 90%? Well, it could actually be basically any percentage. So let's see why.
Imagine I have a vase holding 500k balls, 90% (450k) of which are blue. Now I sample 20 of those balls -completely at random. Could I sample 6 blue and 14 red balls from such a vase? The figure below illustrates the idea.
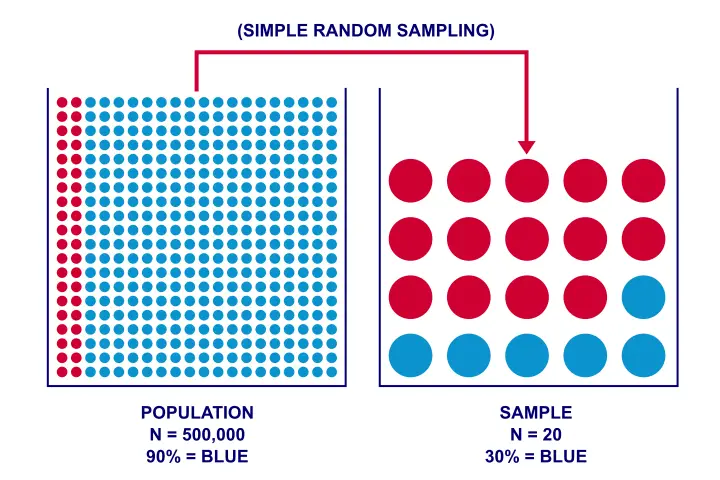
As you can readily see: of course I could sample 6 blue and 14 red balls. My sample of N = 20 balls does not allow me to conclude with certainty that the vase does not contain 90% blue balls.
Now what if my vase contains only 10% blue balls? If I’d sample 20 balls from this vase, could I find 6 blue ones? You’ll probably realize that this is possible indeed.
In short: sampling 6 blue and 14 red balls is possible if 10% or 90% of all balls are blue. It does not rule out either possibility with certainty. So when it comes to concluding anything about my population, a sample is pretty worthless, right?
Wrong.
Thought Experiment: Repeated Sampling
Sure: in theory I could sample 6 blue and 14 red balls from a vase holding 90% blue balls. But it’s practically impossible: the chance is roughly 1 to 4.500,000,000. My small sample basically guarantees that the population percentage is not 90% (but probably much lower).
One way to discover this, is simply trying out the following brute force approach:
- create a fake dataset holding 450k blue and 50k red balls,
- have your computer sample 20 of those 500k balls,
- compute the percentage of blue balls in your sample and
repeat this process 10,000 times. The diagram below visualizes this thought experiment of repeated sampling.
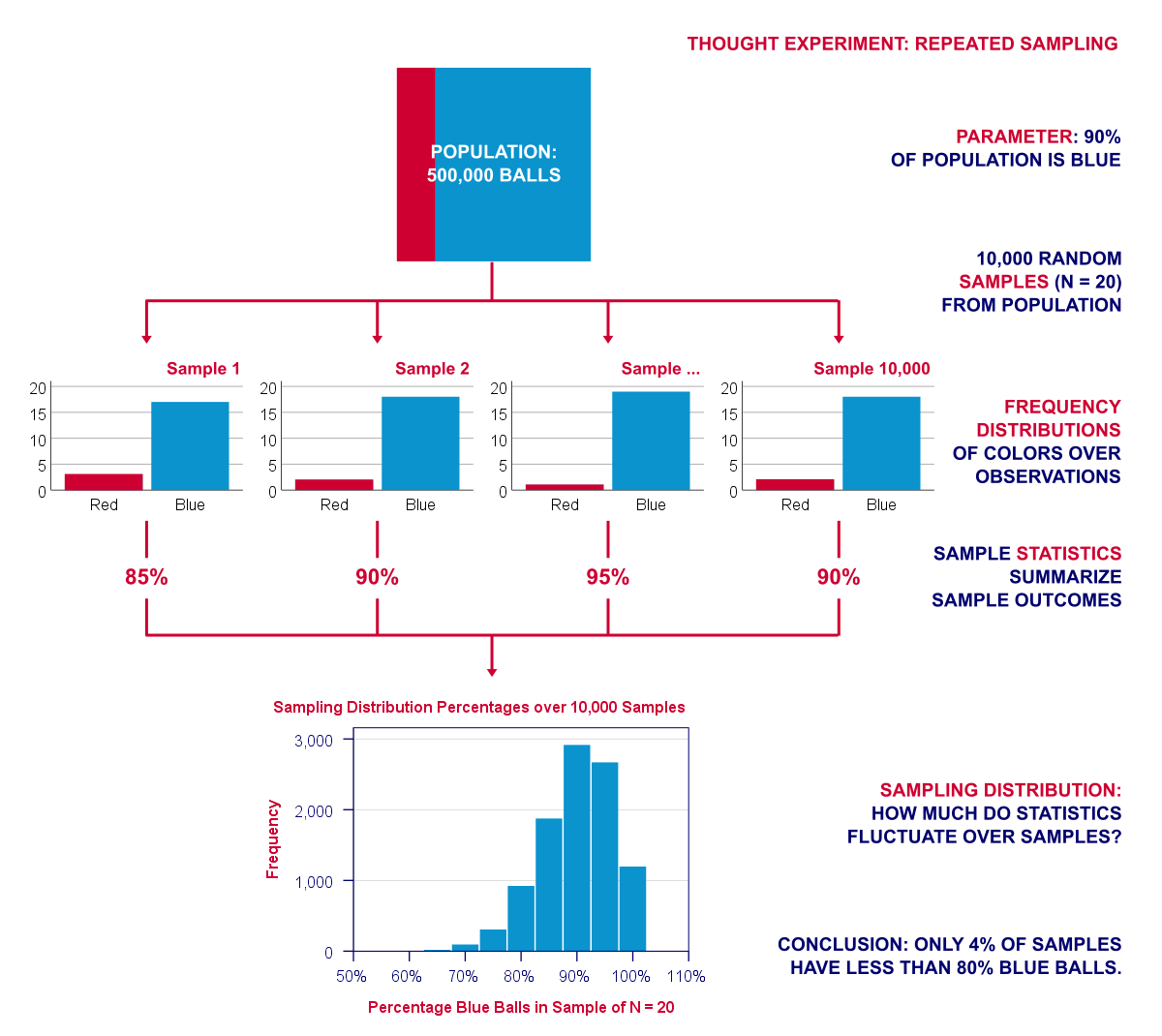
Note that our experiment involves 2 types of frequency distributions. Within each sample, the colors of the balls have a frequency distribution over observations. We can summarize it with a percentage. But here it comes: this percentage -in turn- has a frequency distribution over repeated samples: a sampling distribution.
In a similar vein, correlations, standard deviations and many other statistics also have sampling distributions. And these are useful because they give an idea how much some statistic is likely to be off. This basic reasoning underlies both significance testing and confidence intervals.
Main Sampling Distributions
The sampling distribution we saw -the binomial distribution- isn't used in practice very often. The main sampling distributions* that you will encounter most are
- the (standard) normal distribution;
- the t distribution;
- the F-distribution;
- the chi-square distribution;
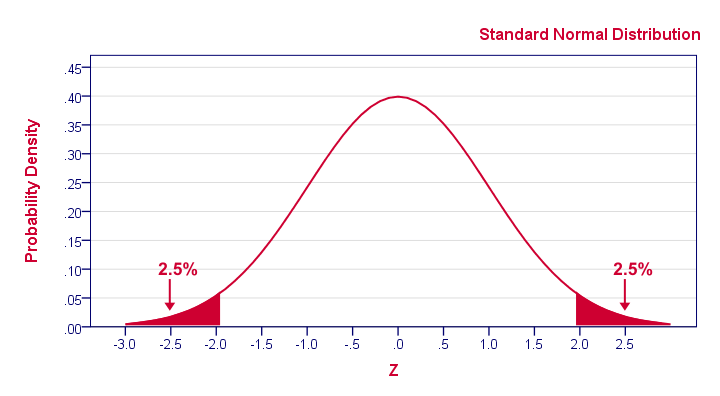
Although it may look different than our binomial distribution, the previous figure conveys the same basic information: some 2.5% of repeated samples should come up with z < -1.96. That is, p(z < -1.96) = 0.025.
Where Can I Get A Sampling Distribution?
Earlier on, we simulated a sampling distribution by having our computer draw 10,000 samples from a dataset containing some population. Although this is a nice and intuitive approach, we don't usually do this. Instead, the sampling distributions for many different statistics -means, correlations, proportions and many others- have been discovered and formulated mathematically. These formulas have been implemented in a lot of software such as MS Excel, OpenOffice and Google Sheets.
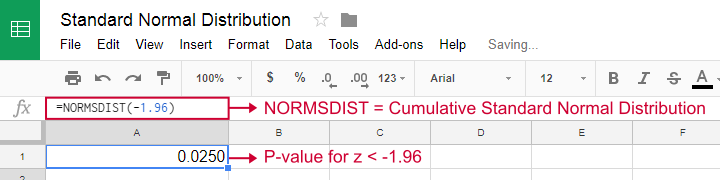
Obviously, all major sampling distributions have also been included in statistical software such as SPSS, Stata and SAS. These packages calculate p-values and confidence intervals straight away for you. So you'll probably skip the sampling distributions altogether in this case.
So What Does The Sampling Distribution Say?
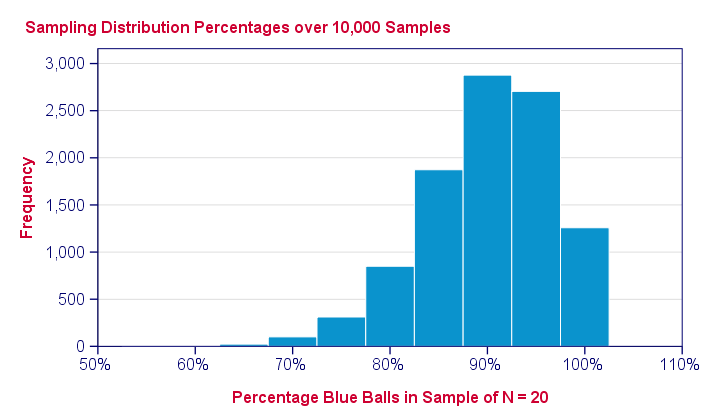
The previous figure shows the sample percentages over 10,000 computerized samples from a population with 90% red balls. So how does that help us? Well, it shows how sample outcomes will fluctuate over samples, given a presumed population percentage.
They don't fluctuate much: the vast majority -some 96%- of sample percentages fall between 80% and 100%. These are likely outcomes; if our population percentage really is 90%, then a sample should probably contain 80% - 100% blue balls. If it doesn't, then the population percentage probably wasn't 90% after all.
So precisely how unlikely are the other outcomes? Well,
- only 4.4% of our 10,000 samples come up with a percentage of 75% or lower;
- only 0.3% come up with 65% or lower;
- the lowest sample percentage is 55% (only 1 sample).
Special Considerations
A population or one sample set of numbers will have a normal distribution. However, because a sampling distribution includes multiple sets of observations, it will not necessarily have a bell-curved shape.
Following our example, the population average weight of babies in North America and in South America has a normal distribution because some babies will be underweight (below the mean) or overweight (above the mean), with most babies falling in between (around the mean). If the average weight of newborns in North America is seven pounds, the sample mean weight in each of the 12 sets of sample observations recorded for North America will be close to seven pounds as well.
However, if you graph each of the averages calculated in each of the 1,200 sample groups, the resulting shape may result in a uniform distribution, but it is difficult to predict with certainty what the actual shape will turn out to be. The more samples the researcher uses from the population of over a million weight figures, the more the graph will start forming a normal distribution.
- Log in to post comments