Normal Distribution
A normal distribution is a bell-shaped frequency distribution curve. Most of the data values in a normal distribution tend to cluster around the mean. The further a data point is from the mean, the less likely it is to occur. There are many things, such as intelligence, height, and blood pressure, that naturally follow a normal distribution. For example, if you took the height of one hundred 22-year-old women and created a histogram by plotting height on the x-axis, and the frequency at which each of the heights occurred on the y-axis, you would get a normal distribution.
The normal distribution, also known as the Gaussian distribution, would be the most important continuous distribution.
For ,
,
the normal distribution is denoted by N(μ,σ2), and its probability density is given by
Characteristics of Normal Distribution
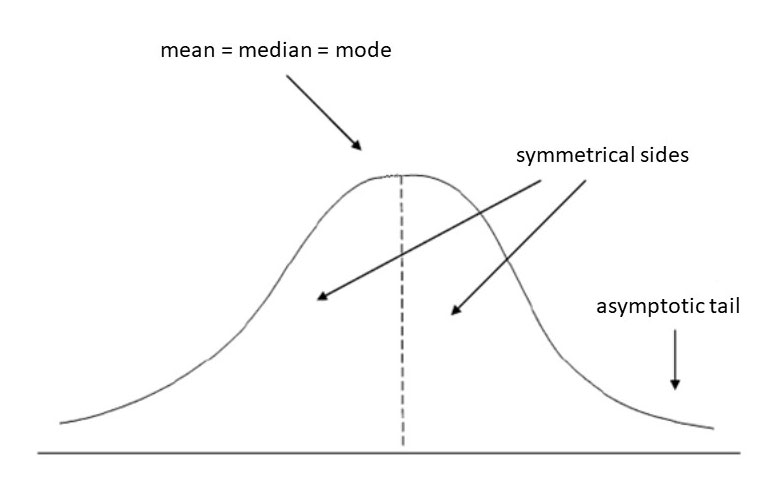
Here, we see the four characteristics of a normal distribution. Normal distributions are symmetric, unimodal, and asymptotic, and the mean, median, and mode are all equal.
A normal distribution is perfectly symmetrical around its center. That is, the right side of the center is a mirror image of the left side. There is also only one mode, or peak, in a normal distribution. Normal distributions are continuous and have tails that are asymptotic, which means that they approach but never touch the x-axis. The center of a normal distribution is located at its peak, and 50% of the data lies above the mean, while 50% lies below. It follows that the mean, median, and mode are all equal in a normal distribution.
The normal distribution is a continuous probability distribution that is symmetrical on both sides of the mean, so the right side of the center is a mirror image of the left side.
The area under the normal distribution curve represents probability and the total area under the curve sums to one.
Most of the continuous data values in a normal distribution tend to cluster around the mean, and the further a value is from the mean, the less likely it is to occur. The tails are asymptotic, which means that they approach but never quite meet the horizon (i.e. x-axis).
For a perfectly normal distribution the mean, median and mode will be the same value, visually represented by the peak of the curve.
The normal distribution is often called the bell curve because the graph of its probability density looks like a bell. It is also known as called Gaussian distribution, after the German mathematician Carl Gauss who first described it.
Why the normal distribution is important:
The bell-shaped curve is a common feature of nature and psychology
The normal distribution is the most important probability distribution in statistics because many continuous data in nature and psychology displays this bell-shaped curve when compiled and graphed.
For example, if we randomly sampled 100 individuals we would expect to see a normal distribution frequency curve for many continuous variables, such as IQ, height, weight and blood pressure.
Parametric significance tests require a normal distribution of the samples' data points
The most powerful (parametric) statistical tests used by psychologists require data to be normally distributed. If the data does not resemble a bell curve researchers may have to use a less powerful type of statistical test, called non-parametric statistics.
Converting the raw scores of a normal distribution to z-scores
We can standardized the values (raw scores) of a normal distribution by converting them into z-scores.
This procedure allows researchers to determine the proportion of the values that fall within a specified number of standard deviations from the mean (i.e. calculate the empirical rule).
- Log in to post comments