“Inferential statistics” is the branch of statistics that deals with generalizing outcomes from (small) samples to (much larger) populations.
Introduction
Statistics has a significant part in the field of data science. It helps us in the collection, analysis and representation of data either by visualisation or by numbers into a general understandable format. Generally, we divide statistics into two main branches which are Descriptive Statistics and Inferential Statistics. In this article, we will discuss the Inferential statistics in detail.
Statistics is one of the most important skills required by a data scientist. There is a lot of mathematics involved in statistics and it can be difficult to grasp. So in this tutorial we are going to go through some of the concepts of statistsics to learn and understand inferential statistics and master it.
Why do we need inferential statistics?
Consider the case where you are interested in the average number of hours children watch television per day. Now you know that the children in your locality on an average watch television for 1 hour per day. How do you go about finding this for all the children?
There are 2 methods you could use to calculate the results:
- Collect data about each and every child.
- Use the data we have to calculate the overall average.
The first method is extremely difficult and daunting task. The amount of effort and resources required to complete this task would be enormous.
The second method is much simpler and easier to accomplish. But there is a problem. You cannot equate the average you obtained from a limited data set to the entire population. Consider the case where the children in your locality are more interested in sports so the number of hours they spend on television is significantly lesser than that of the overall population. How do we go about finding the population mean? This is where inferential statistics comes to our rescue.
Statistical Significance
As we saw, 4.4% of many samples show 75% or fewer red balls. Another way of saying this is that 1 sample has a 4.4% (or 0.044) probability of holding 75% or fewer. This probability value (p-value) is often called “statistical significance” in statistical tests. Articles often just call it “p” as in“F(2,87) = 3.7, p = .028”.This basically means that 2.8% of many samples should come up with an F-value of 3.7 or larger, given some assumptions (including a null hypothesis).
Now let's try it: we'll feed SPSS a sample of N = 20 cases, 75% of which are blue. And now we'll test the null hypothesis that the population percentage = 90%. The result -shown below- confirms that p -denoted by “Exact Sig. (1-tailed)”- is indeed very close to 0.044.

So -again- the p-value of 0.043 means that some 4.3% of many samples should come up with a percentage of 75% or less if the population percentage is 90%. A (rather arbitrary) convention is that we reject the null hypothesis if p < 0.05: if the probability of a sample outcome is less than 5%, then it is so unlikely that we no longer believe that the population percentage is 90%.
What is Inferential Statistics?
Many statistical techniques have been developed to help scientists make sense of the data they collect. These techniques are typically categorized as either descriptive or inferential. While descriptive statistics allow scientists to quickly summarize the major characteristics of a dataset, inferential statistics go a step further by helping scientists uncover patterns or relationships in a dataset, make judgments about data, or apply information about a small dataset to a larger group. They are part of the process of data analysis used by scientists to interpret and make statements about their results .
The inferential statistics toolbox available to scientists is quite large and contains many different methods for analyzing and interpreting data. As an introduction to the topic, we will give a brief overview of some of the more common methods of statistical inference used by scientists. Many of these methods involve using smaller subsets of data to make inferences about larger populations. Therefore, we will also discuss ways in which scientists can mitigate systematic errors (sampling bias) by selecting subsamples (often simply referred to as “samples”) that are representative of the larger population. This module describes inferential statistics in a qualitative way.
Descriptive statistics describe the important characteristics of data by using mean, median, mode, variance etc. It summarises the data through numbers and graphs.
In Inferential statistics, we make an inference from a sample about the population. The main aim of inferential statistics is to draw some conclusions from the sample and generalise them for the population data. E.g. we have to find the average salary of a data analyst across India. There are two options.
- The first option is to consider the data of data analysts across India and ask them their salaries and take an average.
- The second option is to take a sample of data analysts from the major IT cities in India and take their average and consider that for across India.
The first option is not possible as it is very difficult to collect all the data of data analysts across India. It is time-consuming as well as costly. So, to overcome this issue, we will look into the second option to collect a small sample of salaries of data analysts and take their average as India average. This is the inferential statistics where we make an inference from a sample about the population.
In inferential statistics, we will discuss probability, distributions, and hypothesis testing.
Sampling error in inferential statistics
Since the size of a sample is always smaller than the size of the population, some of the population isn’t captured by sample data. This creates sampling error, which is the difference between the true population values (called parameters) and the measured sample values (called statistics).
Sampling error arises any time you use a sample, even if your sample is random and unbiased. For this reason, there is always some uncertainty in inferential statistics. However, using probability sampling methods reduces this uncertainty.
Statistical inference with qualitative data
So far we have only considered examples in which the data being collected and analyzed are quantitative in nature and can be described with numbers. Instead of describing tomato sweetness quantitatively by experimentally measuring the sugar content, what if you asked a panel of taste-testers to rank the sweetness of the tomatoes on a scale from “not at all sweet” to “very sweet”? This would give you a qualitative dataset based on observations rather than numerical measurements .Inferential statistics can be used to analyze more qualitative data like the simulated taste-test data shown above. Statistical methods that compare the shapes of the distributions of the taste-test responses can help determine whether or not the difference in sweetness between the two tomato harvests is statistically significant.
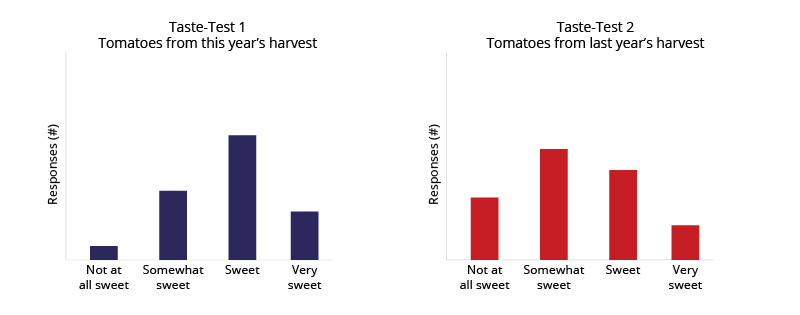
The statistical methods discussed above would not be appropriate for analyzing this kind of data. If you tried to assign numerical values, one through four, to each of the responses on the taste-test scale, the meaning of the original data would change. For example, we cannot say with certainty that the difference between “3 - sweet” and “4 - very sweet” is really exactly the same as the difference between “1 - not at all sweet” and “2 - somewhat sweet.”
Rather than trying to make qualitative data more quantitative, scientists can use methods in statistical inference that are more appropriate for interpreting qualitative datasets. These methods often test for statistical significance by comparing the overall shape of the distributions of two or more subsamples – for instance, the location and number of peaks in the distribution or overall spread of the data – instead of using more quantitative measures like the mean and standard deviation. This approach is perfect for analyzing your tomato taste-test data. By using a statistical test that compares the shapes of the distributions of the taste-testers’ responses, you can determine whether or not the results are significantly different and thus whether one tomato harvest actually tastes sweeter than the other.
Proceed with caution!
Inferential statistics provides tools that help scientists analyze and interpret their data. The key here is that the scientists – not the statistical tests – are making the judgment calls. The way that the term “significance” is used in statistical inference can be a major source of confusion. In statistics, significance indicates how reliably a result can be observed if a statistical test is repeated over and over. A statistically significant result is not necessarily relevant or important; it is the scientist that determines the importance of the result.
One additional pitfall is the close relationship between statistical significance and subsample size. As subsamples grow larger, it becomes easier to reliably detect even the smallest differences among them. Sometimes well-meaning scientists are so excited to report statistically significant results that they forget to ask whether the magnitude, or size, of the result is actually meaningful.
Statistical inference is a powerful tool, but like any tool it must be used appropriately. Misguided application or interpretation of inferential statistics can lead to distorted or misleading scientific results. On the other hand, proper application of the methods described in this module can help scientists gain important insights about their data and lead to amazing discoveries. So use these methods wisely, and remember: It is ultimately up to scientists to ascribe meaning to their data.
Final Notes
Right, so inferential statistics basically tries to show how sample outcomes fluctuate over samples. If a statistic fluctuates little, then we can be reasonably confident that it's close to the population parameter that we're after. I hope this quick tutorial gave you a basic idea of how it works.
In this article, we studied inferential statistics and the different topics in it like probability, hypothesis testing, and different types of tests in hypothesis. Also, we discussed the importance of inferential statistics and how we can make inference about the population by sample data which in turn is time-consuming and cost-saving.Many techniques have been developed to aid scientists in making sense of their data. This module explores inferential statistics, an invaluable tool that helps scientists uncover patterns and relationships in a dataset, make judgments about data, and apply observations about a smaller set of data to a much larger group. The module explains the importance of random sampling to avoid bias. Other concepts include populations, subsamples, estimation, and the difference between a parameter and a statistic.
- Log in to post comments