
The method in which we select samples to learn more about characteristics in a given population is called hypothesis testing.
Hypothesis testing is really a systematic way to test claims or ideas about a group or population.
To test whether this claim is true, we record the time (in hours) that a group of 20 American children (the sample), among all children in the United States (the population), watch TV. The mean we measure for these 20 children is a sample mean. We can then compare the sample mean we select to the population mean stated in the article.
Hypothesis testing or significance testing is a method for testing a claim or hypothesis about a parameter in a population, using data measured in a sample. In this method, we test some hypothesis by determining the likelihood that a sample statistic could have been selected, if the hypothesis regarding the population parameter were true.
In an example, if we select a random sample from this population with a mean of 1,000, then on average, the value of a sample mean will equal 1,000. On the basis of the central limit theorem, we know that the probability of selecting any other sample mean value from this population is normally distributed. In behavioral research, we select samples to learn more about populations of interest to us. In terms of the mean, we measure a sample mean to learn more about the mean in a population. Therefore, we will use the sample mean to describe the population mean. We begin by stating the value of a population mean, and then we select a sample and measure the mean in that sample. On average, the value of the sample mean will equal the population mean. The larger the difference or discrepancy between the sample mean and population mean, the less likely it is that we could have selected that sample mean, if the value of the population mean is correct.
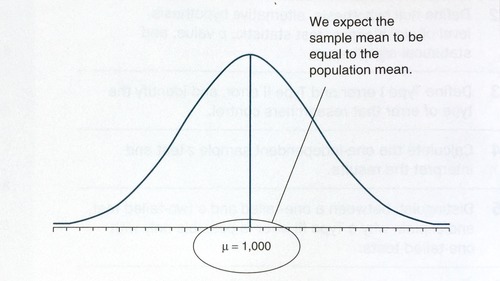
The sampling distribution for a population mean is equal to 1,000. If 1,000 is the correct population mean, then we know that, on average, the sample mean will equal 1,000 (the population mean). Using the empirical rule, we know that about 95% of all samples selected from this population will have a sample mean that falls within two standard deviations (SD) of the mean. It is therefore unlikely (less than a 5% probability) that we will measure a sample mean beyond 2 SD from the population mean, if the population mean is indeed correct.
Type I error and Type II error:
No hypothesis test is 100% certain. Because the test is based on probabilities, there is always a chance of making an incorrect conclusion. When you do a hypothesis test, two types of errors are possible: type I and type II. The risks of these two errors are inversely related and determined by the level of significance and the power for the test. Therefore, you should determine which error has more severe consequences for your situation before you define their risks.
Basis for comparison | Type I error | Type II error |
| Definition | Type 1 error, in statistical hypothesis testing, is the error caused by rejecting a null hypothesis when it is true. | Type II error is the error that occurs when the null hypothesis is accepted when it is not true. |
| Also termed | Type I error is equivalent to false positive. | Type II error is equivalent to a false negative. |
| Meaning | It is a false rejection of a true hypothesis. | It is the false acceptance of an incorrect hypothesis. |
| Symbol | Type I error is denoted by α. | Type II error is denoted by β. |
| Probability | The probability of type I error is equal to the level of significance. | The probability of type II error is equal to one minus the power of the test. |
| Reduced | It can be reduced by decreasing the level of significance. | It can be reduced by increasing the level of significance. |
| Cause | It is caused by luck or chance. | It is caused by a smaller sample size or a less powerful test. |
| What is it? | Type I error is similar to a false hit. | Type II error is similar to a miss. |
| Hypothesis | Type I error is associated with rejecting the null hypothesis. | Type II error is associated with rejecting the alternative hypothesis. |
| When does it happen? | It happens when the acceptance levels are set too lenient. | It happens when the acceptance levels are set too stringent. |
The method of hypothesis testing.
1. To begin, we identify a hypothesis or claim that we feel should be tested. For example, we might want to test the claim that the mean number of hours that children in the United States watch TV is 3 hours.
2. We select a criterion upon which we decide that the claim being tested is true or not. For example, the claim is that children watch 3 hours of TV per week. Most samples we select should have a mean close to or equal to 3 hours if the claim we are testing is true. So at what point do we decide that the discrepancy between the sample mean and 3 is so big that the claim we are testing is likely not true? We answer this question in this step of hypothesis testing.
3. Select a random sample from the population and measure the sample mean. For example, we could select 20 children and measure the mean time (in hours) that they watch TV per week.
4. Compare what we observe in the sample to what we expect to observe if the claim we are testing is true. We expect the sample mean to be around 3 hours. If the discrepancy between the sample mean and population mean is small, then we will likely decide that the claim we are testing is indeed true. If the discrepancy is too large, then we will likely decide to reject the claim as being not true.
- Log in to post comments