An F statistic is a value you get when you run an ANOVA test or a regression analysis to find out if the means between two populations are significantly different. It’s similar to a T statistic from a T-Test; A-T test will tell you if a single variable is statistically significant and an F test will tell you if a group of variables are jointly significant.
Testing Multiple Linear Restrictions: The F-test
Three situations call for this test Testing exclusion restrictions. Example: Does the genre of background music affect sales at Mitchell’s ice cream? Testing the overall significance of a regression. Testing more complicated general linear restrictions motivated by a model.
Testing Multiple Linear Restrictions: The F-test
Two ways to calculate F-statistic : Using SSR : Using R-sq :Equivalent because ?? ? ? =TSS 1− ? ? 2 and ?? ? ? =TSS 1− ? ? 2How to remember which one comes first in the numerator? Remember that the F-statistic is always >0, so the one that is larger comes first. Note: When taking R-squared from Stata output to put it in this formula, do NOT square it! ?= ( ? ? 2 − ? ? 2 )/? (1− ? ? 2 )/(?−?−1)
Testing Multiple Linear Restrictions: The F-test
Test of the overall significance of a regression. The test of overall significance is reported in most regression packages; the null hypothesis is usually overwhelmingly rejected. The null hypothesis states that the explanatory variables are not useful at all in explaining the dependent variable Restricted model(regression on constant)
More use of the F-test Testing general linear restrictions with the F-test Example: Test whether house price assessments are rational. The assessed housing value (before the house was sold)Size of lot(in feet)Actual house price Square footage Number of bedrooms. In addition, other known factors should not influence the price once the assessed value has been controlled for. If house price assessments are rational, a 1% change in the assessment should be associated with a 1% change in price.
The F-test for overall significance has the following two hypotheses:
- The null hypothesis states that the model with no independent variables fits the data as well as your model.
- The alternative hypothesis says that your model fits the data better than the intercept-only model.
To calculate the F-test of overall significance, your statistical software just needs to include the proper terms in the two models that it compares. The overall F-test compares the model that you specify to the model with no independent variables. This type of model is also known as an intercept-only model.
Using The F Statistic
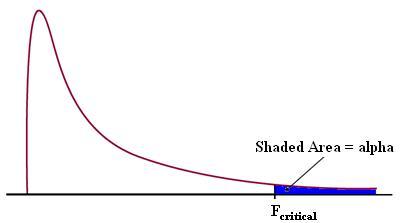
You can use the F statistic when deciding to support or reject the null hypothesis. In your F test results, you’ll have both an F value and an F critical value.
- The F critical value is also called the F statistic.
- The value you calculate from your data is called the F value (without the “critical” part).
In general, if your calculated F value in a test is larger than your F statistic, you can reject the null hypothesis. However, the statistic is only one measure of significance in an F Test. You should also consider the p value. The p value is determined by the F statistic and is the probability your results could have happened by chance.
Why?
The F value should always be used along with the p value in deciding whether your results are significant enough to reject the null hypothesis. If you get a large f value (one that is bigger than the F critical value found in a table), it means something is significant, while a small p value means all your results are significant. The F statistic just compares the joint effect of all the variables together. To put it simply, reject the null hypothesis only if your alpha level is larger than your p value.
In linear regression, the F-test can be used to answer the following questions:
- Will you be able to improve your linear regression model by making it more complex i.e. by adding more linear regression variables to it?
- If you already have a complex regression model, would you be better off trading your complex model with the intercept-only model (which is the simplest linear regression model you can build)?
The second question is a special case of the first question. In both cases, the two models are said to be nested. The simpler model is called the restricted model. It is as if we are restricting it to use fewer regression variables. The complex model is called the unrestricted model. It contains all the variables of the restricted model and at least one more variable. The restricted model is said to be nested within the unrestricted model.
- Log in to post comments